Factors Affecting Magnetic Field Strength Around a Straight Conductor
Explore the principles behind the magnetic field due to a current through a straight conductor, an essential topic in electricity and magnetism for both class 10 and advanced Physics. Understand its definition, formula, diagram, derivation, and practical relevance to excel in exams and real-world applications. Read on to discover the science and experiments behind this fascinating effect.
Understanding the Magnetic Field Due to a Current Through a Straight Conductor
When an electric current flows through a straight conductor, such as a wire, it generates a magnetic field around it. This fundamental magnetic field due to a current through a straight conductor is one of the cornerstones of electromagnetism in Physics. The concept is important in explaining how electric currents can create magnetic effects, seen not just in educational settings but also in practical devices ranging from electric motors to power transmission lines.
The magnetic field lines produced by a straight current-carrying conductor form concentric circles centered at the wire. The direction of these circles is determined by the direction of current flow, which can be easily remembered using the right-hand thumb rule: point the thumb of your right hand in the direction of the current, and your curled fingers show the direction of the magnetic field.
This principle was first demonstrated experimentally by Hans Christian Oersted, whose work opened the door to the field of electromagnetism. To further clarify, the magnetic field due to a current through a straight conductor class 10 curriculum highlights this effect and its diagrammatic representation, forming the basis for electromagnet design and electromagnetic induction.
Definition and Key Features
The magnetic field due to a current through a straight conductor definition states: "When an electric current passes through a straight conductor, it creates a magnetic field in the surrounding space, the field consisting of circular lines of force centered on the wire." These circular field lines are known as concentric circles.
- Field lines are concentric around the conductor.
- The direction follows the right-hand thumb (current direction = thumb, field = curled fingers).
- Strength of the field depends on current and distance from the wire.
Experimentally, this can be verified by placing a magnetic compass near a straight current-carrying wire and observing the compass needle's deflection, as commonly demonstrated in school labs (magnetic field due to a current through a straight conductor experiment).
Formula for Magnetic Field Due to a Straight Current-Carrying Conductor
The magnitude of the magnetic field due to a current through a straight conductor depends on the amount of current and the distance from the wire. For an infinitely long straight wire, the formula is:
Where:
- $B$ = Magnetic field strength (Tesla, T)
- $\mu_0$ = Permeability of free space ($4\pi \times 10^{-7}$ T·m/A) (see permeability details)
- $I$ = Current through the conductor (Ampere, A)
- $r$ = Radial distance from the wire (meters, m)
This formula reflects that the magnetic field due to a current carrying conductor decreases as you move farther from the wire and increases with greater current. As such, the magnetic field due to a current through a straight conductor depends upon both current magnitude and radial distance.
Derivation: Step-by-Step
Let’s see the magnetic field due to a current through a straight conductor derivation using the Biot-Savart Law:
- Begin with Biot–Savart Law, which states that the infinitesimal magnetic field $d\vec{B}$ at a point due to a small current element $I d\vec{l}$ is: $$ d\vec{B} = \frac{\mu_0}{4\pi} \frac{I d\vec{l} \times \hat{r}}{r^2} $$
- For a straight, infinitely long wire, integrate along the length considering the perpendicular distance, simplifying the cross-product and integrating over $\theta$ from $-\pi/2$ to $+\pi/2$.
- The integral gives: $$ B = \frac{\mu_0 I}{2\pi r} $$
Thus, the magnetic field due to an infinitely long straight wire class 12 is derived, providing an exact mathematical approach suited for advanced learners and competitive exams. These derivations also support a clear magnetic field due to straight current carrying conductor graph—a curve that shows $B$ is inversely proportional to $r$.
Visualization: Diagrams & Direction
For clarity, a magnetic field due to a current through a straight conductor diagram is often used in textbooks and exams. The concentric circles around the wire indicate field lines, with arrows showing direction (using the right-hand rule).
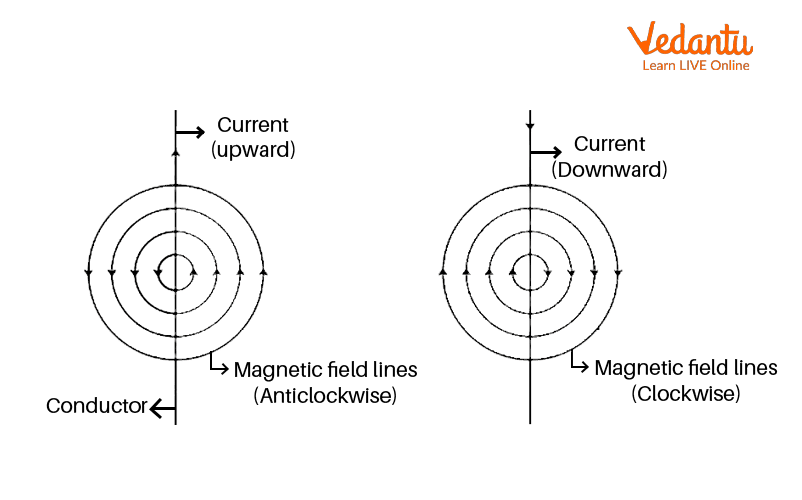
If the current flows upward, the magnetic field lines move counterclockwise when viewed from above and clockwise for a downward current.
Practical Examples and Applications
Let’s apply these principles with a typical numerical example—used frequently in both class 10 and class 12 Physics:
- A wire carries a current of $5\ \text{A}$. What is the magnetic field at a point $2\ \text{cm}$ ($0.02\ \text{m}$) from the wire?
Using the formula: $B = \frac{\mu_0 I}{2\pi r} = \frac{4\pi \times 10^{-7} \times 5}{2\pi \times 0.02} = \frac{20\pi \times 10^{-7}}{2\pi \times 0.02}$
Simplify to get: $B = \frac{10^{-6} \times 5}{0.02} = 2.5 \times 10^{-5}\ \text{T}$
Practical applications of this law are seen in devices relying on electromagnetism, like electric bells, maglev trains, and various sensors. The principles of magnetic effects of electric current and the force on a current-carrying conductor in a magnetic field (as covered in Class 10 and 12 topics) are built directly upon this concept.
Summary Table: Key Quantities and Relationships
| Quantity | Symbol | Unit |
|---|---|---|
| Magnetic Field Strength | $B$ | Tesla (T) |
| Current | $I$ | Ampere (A) |
| Distance from Wire | $r$ | Meter (m) |
| Permeability of Free Space | $\mu_0$ | $4\pi \times 10^{-7}$ T·m/A |
This table helps in quick revisions, especially for exam-oriented problems where relationships between the quantities are crucial.
How the Magnetic Field Strength Varies
A crucial aspect in the magnetic field due to a current through a straight conductor explanation is its dependency. The field strength is directly proportional to the current and inversely proportional to the distance from the conductor. For comparison, the field near a circular current loop or a solenoid differs in geometry and magnitude, which is explored in more advanced studies.
Conclusion: Significance in Physics and Beyond
The magnetic field due to a current through a straight conductor remains one of the most important principles in classical and modern Physics. Whether studying the basics in class or delving into college-level electromagnetism, this topic underpins technologies from generators to medical equipment. For deeper insights into electromagnetism and related laws like Biot–Savart Law and Faraday’s Law, explore more in our concept-rich Physics sections at Vedantu.
FAQs on Understanding the Magnetic Field Created by a Current Through a Straight Wire
1. What is the magnetic field due to a current through a straight conductor?
The magnetic field due to a current through a straight conductor is the region where magnetic effects are detected around the conductor when electric current flows through it.
- The field forms concentric circles around the wire.
- The strength of the field increases with increased current and decreases with distance from the wire.
- This phenomenon is explained by Oersted’s experiment.
2. How does the direction of the magnetic field relate to current flow in a straight conductor?
The direction of the magnetic field around a straight conductor is given by the famous Right Hand Thumb Rule.
- If you hold the conductor in your right hand with the thumb pointing in the direction of current, then your curled fingers show the direction of the magnetic field lines.
3. What happens to the magnetic field if the current in the straight conductor is doubled?
Doubling the current through a straight conductor directly doubles the magnetic field strength around it.
- Magnetic field (B) is proportional to the current (I).
- B ∝ I
4. How does distance from the wire affect the magnetic field strength?
The magnetic field strength produced by a current-carrying straight wire decreases as distance increases.
- Magnetic field (B) is inversely proportional to the distance (r) from the wire.
- B ∝ 1/r
5. Describe Oersted’s experiment and its significance for the magnetic field around a straight conductor.
Oersted’s experiment demonstrated that an electric current produces a magnetic field.
- He placed a magnetic compass near a current-carrying wire and observed deflection of the needle.
- This proved the direct connection between electricity and magnetism.
- It formed the basis of electromagnetism.
6. State the Right Hand Thumb Rule for the direction of magnetic field due to a straight conductor.
The Right Hand Thumb Rule helps find the direction of magnetic field lines.
- Point the thumb of your right hand in the direction of the current.
- The direction in which your fingers wrap around the conductor shows the direction of magnetic field lines.
7. What factors affect the strength of the magnetic field produced by a straight current-carrying conductor?
The strength of the magnetic field is affected by:
- The magnitude of current (more current, stronger field).
- The distance from the conductor (closer, stronger field).
- Nature of conductor and surrounding medium (e.g., presence of ferromagnetic materials enhances field).
8. What is the shape of magnetic field lines around a straight current-carrying wire?
The magnetic field lines around a straight current-carrying conductor form concentric circles centered on the wire.
- The field is strongest close to the wire and weakens with distance.
9. Why is understanding the magnetic field around a straight conductor important in physics?
Understanding the magnetic field around a straight conductor is essential for many electrical devices and concepts.
- It explains the working of electromagnets, motors, and generators.
- Lays the foundation for studying electromagnetism and its applications.
10. What is the mathematical expression for the magnetic field at a distance r from a long straight conductor carrying current I?
The magnetic field (B) at distance r from a long straight conductor carrying current I is given by:
- B = (μ₀/2π) × (I/r), where μ₀ = permeability of free space.
- This formula shows that B increases with I and decreases as r increases.
11. Name the rule used to determine the direction of magnetic field around a straight conductor.
Right Hand Thumb Rule is used to determine the direction of magnetic field around a straight conductor carrying current.
- Point your right thumb in current’s direction; curled fingers show magnetic field direction.
12. What is observed when a magnetic compass is placed near a current-carrying straight conductor?
When a magnetic compass is placed near a current-carrying straight conductor, the compass needle gets deflected.
- This deflection confirms the presence and direction of the magnetic field generated by electric current, as demonstrated in Oersted’s experiment.